GMAT Ratio And Proportion Tricks – Simple Ways To Solve
If you’re preparing for the GMAT, you would know that ratios and proportions are essential concepts to master in Quantitative Reasoning. They frequently appear on the test, and you need to be able to solve them quickly and accurately. Fortunately, some methods can help you tackle these problems with ease. This blog post will cover some of the most valuable techniques, along with examples, for ratios and proportions on the GMAT.
Take Free GMAT 2023 Daily Targets
Subscribe To GMAT Preparation Channel
Technique 1: Approximations
Q1. For every 7 tons of ore processed, 0.48 ounces of gold is recovered. How many tons of ore must be processed to recover 60 ounces of gold?
A. 201
B. 219
C. 438
D. 805
E. 875
A: Since you have to calculate the answer without a calculator, approximation is the way to go.
We know that:
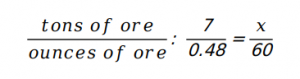

We know that the latter is 840. Hence the answer should be more than that. Hence E is the correct option.
Technique 2: Forming Equations
Q2. Evaluate the problem and the two statements – labelled (1) and (2) – that contain certain data or information. Using the given statements, decide whether the information provided is sufficient to answer the question.
What is the total number of students in the class?
Statement 1: The number of girls in the class is 4 more than the number of boys.
Statement 2: The number of boys is 355of the number of girls.
A: Let the number of boys be b and the number of girls be g
From statement 1, there are 44 more girls than boys, hence b = g – 4.
This statement is not sufficient.
From statement 2, the number of boys is 3/5 the number of girls –> b = 3/5g
This statement is not sufficient.
From both statements, we have two distinct linear equations with two unknowns, thus we can solve for b and g and get the total number of students (b+g).
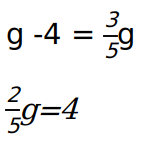
Hence g =10, b= 6
Technique 3: Reducing Ratios to Simple Terms
Q3.A box contains Rs. 500 in the form of one rupee, 50p and 25p coins in the ratio of 3:2:4. Then find the number of 50p coins in the box?
A) 400
B) 200
C) 500
D) 100
E) 300
A: The value of 1 Rupee: 50p: 25p= 1:0.5:0.25
Number of 1 Rupee: 50p: 25p coins= 3:2:4
Ratio of coins by value= 3:1:1
Hence value of 50p coins= 1/5 of total value= 100
Notice that in the first step we could have written the ratio as 4:2:1 instead of 1:0.5:0.25, however, the latter method simplifies the problem because we are able to express the ratio of coins by value through a convenient ratio.
In conclusion, these methods can be incredibly helpful when working with ratios and proportions on the GMAT. By mastering these techniques, you can save time and avoid mistakes, allowing you to focus on the more challenging questions on the exam.
A simple way to master these techniques is to practice questions on a regular basis. Do take these FREE GMAT Daily Tests, which come with detailed video solutions, to practice GMAT questions.
All the best.
Also Read:
- What Is GMAT? – Everything to know about the test
- How To Prepare For GMAT In 1 Month?
- What Is Tested In GMAT Verbal? How To Improve Verbal In GMAT?
- Introduction To GMAT Verbal Reasoning (With Solved Examples)
- How To Improve In GMAT Sentence Correction: Tips, Tricks, and Strategies
- 6 Interesting Facts About The GMAT Exam You Should Know
- GMAT preparation for beginners: What to Study and How
- 6 Best Practices for GMAT Preparation: The Ultimate Study Guide
- How To Study For GMAT With Full-time Job?
- Can You Study for GMAT On Your Own? A Step-by-step Approach
- Is GMAT Easy To Crack? What Makes GMAT Challenging
- How to start your GMAT preparation | 5 Tips To Crack GMAT
- Top colleges accepting GMAT scores in India
If you are starting your GMAT preparation from scratch, you should definitely check out the GMATPOINT
