GMAT Algebraic Expressions Questions With Solutions PDF

GMAT Algebraic Expressions Questions 2025
GMAT Algebraic Expressions questions are an important part of the GMAT Quant section. These questions test how well you can simplify, factor, and evaluate expressions, especially in real-life situations like cost calculations, distance-time problems, investments, or finding unknowns.
You might get algebra expression questions alone or as part of longer word problems or Data Sufficiency questions. The good news is, they are easy once you know the basic rules of simplifying and rearranging terms. You don’t need high-level math, just careful steps and a strong understanding of algebra rules. Practice with a GMAT mock test to understand the exam pattern.
In this blog, you’ll find a simple rule PDF, a set of practice questions with answers, and a few additional problems to improve your confidence before the exam. You’ll also learn about common mistakes students make and smart time-saving tricks.
Important Rules for GMAT Algebraic Expressions
You only need a few rules to solve algebra questions. These rules help you simplify expressions and find values correctly.
| Concept | Formula / Explanation |
|---|---|
| Like Terms | Combine only terms with the same variable and power: Example → 3x + 4x = 7x |
| Distributive Property | a(b + c) = ab + ac Example → 2(x + 5) = 2x + 10 |
| Factoring Common Terms | Take out the greatest common factor (GCF): Example → 6x + 9 = 3(2x + 3) |
| Difference of Squares | a² − b² = (a + b)(a − b) |
| Perfect Square Trinomial | a² ± 2ab + b² = (a ± b)² |
| Substitution | Replace variables with given values: Example → If x = 2, then 3x + 1 = 7 |
| Rearranging Equations | Move terms to isolate the variable using basic operations. |
| Expanding Brackets | (x + a)(x + b) = x² + (a + b)x + ab |
These rules are useful for cost, speed, age, work, and any problem where you simplify or evaluate algebraic expressions.
Top 5 Common Mistakes to Avoid in GMAT Algebraic Expressions Questions
Students often lose marks due to small misunderstandings about algebra rules. These mistakes mostly happen when solving quickly or not simplifying properly.
Here are the most common ones to avoid:
Adding or subtracting unlike terms: Only combine terms with the same variable and power (e.g., x and x² are not the same).
Forgetting to use the distributive rule: Always multiply everything inside the brackets.
Sign errors: Be careful with plus and minus signs, as they can change everything!
Missing what the question is asking: Sometimes it’s not about solving, just rewriting, or comparing.
Oversimplifying too soon: Some expressions are easier to work with in factored form.
List of GMAT Algebraic Expressions Questions
Here’s a short set of GMAT-style algebraic expression questions to help you practice. They include all common types of simplification, factoring, substitution, and distributive property. Practice these often to become fast and accurate before your GMAT test.
Question 1
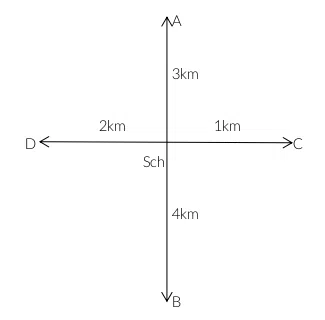
The playgrounds of four school teams - A, B, C and D are located in the North, South, East and West directions with respect to the school in no particular order. A’s and B’s playgrounds are located in opposite directions. D’s ground is located at 90 degrees clockwise direction with respect to B’s playground. The distances of the four playgrounds from the school are 1km, 2km, 3km and 4km in no particular order. D’s playground is located in the west. A’s playground is not the one closest to the school, while C’s playground is closer to the school than D’s playground. The playground located in the south is the farthest from the school. If A’s playground is the one located at a distance of 3km from the school, then how far from the school is the playground located in the west?
correct answer:- 2
Question 2
If $$\dfrac{p}{q}+\dfrac{q}{p}\ =\ 1$$ then the value of $$(p^{3}+q^{3})$$ is
correct answer:- 1
Question 3
If m - 5n = 2, then the vlaue of $$\left(m^3-125n^3-\ 30mn\right)$$ is
correct answer:- 3
Question 4
If $$\frac{4+3\sqrt{3}}{\sqrt{7+4\sqrt{3}}}= A+\sqrt{B}$$, then $$B-A$$ is
correct answer:- 3
Question 5
If $$a^{2}+1=a$$, then the value of $$a^{12}+a^{6}+1$$ is :
correct answer:- 4
Question 6
If $$p- 2q = 4$$, then the value of $$p^{3} - 8q^{3} - 24pq - 64$$ is :
correct answer:- 2
Question 7
If $$x+\frac{1}{x}=2$$ then the value of $$(x^2+\frac{1}{x^2})(x^3+\frac{1}{x^3})$$ is
correct answer:- 2
Question 8
If a, b, c be all positive integers, then the least positive value of $$a^{3} + b^{3} + c^{3} - 3abc$$ is
correct answer:- 3
Question 9
If $$a=\frac{2+\sqrt{3}}{2-\sqrt{3}}$$ and $$b=\frac{2-\sqrt{3}}{2+\sqrt{3}}$$, then the value of $$a^2+b^2+a \times b$$ is
correct answer:- 2
Question 10
If a + b + 1 = 0, then the value of $$(a^3 + b^3 +1 - 3ab)$$ is
correct answer:- 2
Question 11
If $$\frac{3-5x}{x} + \frac{3-5y}{y} + \frac{3-5z}{z} = 0 $$, the value of $$\frac{1}{x} + \frac{1}{y} + \frac{1}{z}$$ is
correct answer:- 2
Question 12
Which of the following options must be added to the expression $$16a^2 -12a$$ to make it a perfect square?
correct answer:- 1
Question 13
Which of the following quadratic equations has equal roots?
correct answer:- 4
Question 14
The Simplified form of $$\frac{(b^{3}x^{2}a^{4}z^{3})\times(b^{4}x^{3}a^{3}z^{2})}{(a^{2}b^{4}z^{3})}$$ is
correct answer:- 3
Question 15
If a + b = 10 and ab = 24, then the value of $$a^3 + b^3$$ is
correct answer:- 1
Question 16
If 5x - 1 < 3x + 2 and 5x + 5 > 6 - 2x; then x can take which of the following values?
correct answer:- 2
Question 17
If $$x - y = -6$$ and $$x + y = 16$$, then $$x^2 - y^2$$ is?
correct answer:- 2
Question 18
Value of $$\dfrac{4a^2+12ab+9b^2}{2a+3b}$$ is
correct answer:- 2
Question 19
If $$(x+y)^{2}=xy+1$$ and $$x^3 - y^3 = 1$$, then what is the value of x - y?
correct answer:- 1
Question 20
What is the value of $$\frac{1+x}{1-x^4}\div\frac{x^2}{1+x^2}\times x(1-x)$$ ?
correct answer:- 1
Question 21
The product of three consecutive odd numbers is 1287. What is the largest of the three numbers?
correct answer:- 3
Question 22
If a + b = 5 and ab = 6, then what is the value of $$a^{3} + b^{3}$$ ?
correct answer:- 3
Question 23
If a = 2 , b = -3 then the value of $$27a^3 - 54a^2b + 36ab^2 - 8b^3$$ is
correct answer:- 4
Question 24
If m + n = 1, then the value of $$m^3 + n^3 + 3mn$$ is equal to
correct answer:- 2
Question 25
If $$( x - 5)^{2}$$ + $$(y - 2)^{2}$$ + $$(z - 9)^{2}$$ = 0 , then value of (x + y - z) is
correct answer:- 3
Question 26
If $$x+\frac{1}{x}=6$$, then value of $$x^{2} + 1/x^{2}$$ is
correct answer:- 3
Question 27
If $$x + y + z = 0$$, then what is the value of $$\dfrac{(3y^2 + x^2 + z^2)}{(2y^2 - xz)}?$$
correct answer:- 1
Question 28
$$x, y$$ and $$z$$ are real numbers. If $$x^3 + y^3 + z^3 = 13,x + y + z = 1$$ and $$xyz = 1$$, then what is the value of $$xy + yz + zx?$$
correct answer:- 4
Question 29
If $$P = 7 + 4\surd3$$ and $$PQ = 1$$, then what is the value of $$\frac{1}{P^2}+\ \frac{1}{Q^2}$$?
correct answer:- 3
Question 30
If $$x - 4y = 0$$ and $$x + 2y = 24$$, then what is the value of $$\dfrac{2x+3y}{2x-3y}$$?
correct answer:- 2
Question 31
If $$(\frac{x}{a}) + (\frac{y}{b}) = 3$$ and $$(\frac{x}{b}) - (\frac{y}{a}) = 9$$, then what is the value of $$\frac{x}{y}$$?
correct answer:- 1
Question 32
If $$x = a + \frac{1}{a} and y = a - \frac{1}{a}$$ then $$\sqrt{x^4 + y^4 - 2x^2y^2}$$ is equal to:
correct answer:- 4
Question 33
If $$(8x^3 - 27y^3) \div (2x — 3y) = (Ax^2 + Bxy + Cy^2)$$, then the value of (2A + B - C) is:
correct answer:- 2
Question 34
If $$(x - 7)^3 + (x - 8)^3 + (x + 6)^3 = 3(x - 7)(x - 8)(x + 6)$$, then what is the value of $$x$$ ?
correct answer:- 2
Question 35
If $$(x^3-y^3):(x^2+xy+y^2)=5:1$$ and $$(x^2-y^2):(x-y)=7:1$$ then the value of $$2x:3y$$ equals
correct answer:- 2
Question 36
If $$a-\dfrac{1}{a-3}=5$$ then the value of $$(a-3)^{3}-\dfrac{1}{(a-3)^{3}}$$
correct answer:- 1
Question 37
If $$a+\frac{1}{b}=b+\frac{1}{c}=c+\frac{1}{a}$$ where as $$a\ne b\ne c\ne0$$ then the value of $$a^{2}b^{2}c^{2}$$ is
correct answer:- 2
Question 38
If $$a^{2} + b^{2}+ c^{2} = 2(a - b - c) - 3$$, then the value of $$a-b+c$$ is
correct answer:- 3
Question 39
If $$x^{a}.x^{b}.x^{c}= 1$$ for all real x, then the value of $$a^{3} + b^{3}+ c^{3}$$ is
correct answer:- 4
Question 40
If $$a^4+a^2b^2+b^4=8$$ and $$a^2+ab+b^2=4$$, then the value of $$ab$$ is
correct answer:- 4
Question 41
If $$a = 25, b = 15, c = -10$$, then the value of $$\dfrac{a^3 + b^3 + c^3 - 3 abc}{(a-b)^2 + (b-c)^2 + (c-a)^2}$$ is
correct answer:- 4
Question 42
If $$a^2+b^2+\dfrac{1}{a^2}+\dfrac{1}{b^2}=4$$ then the value of $$a^{2}+b^{2}$$ will be
correct answer:- 3
Question 43
If $$x^3+3x^2+3x=7$$, then $$x$$ is equal to
correct answer:- 3
Question 44
If $$x^2 + y^2 - 2x + 6y + 10 = 0$$, then the value of $$(x^2 + y^2)$$ is
correct answer:- 4
Question 45
What is the Simplified value of:
$$\frac{1}{8}\left\{\left(x + \frac{1}{y}\right)^2 - \left(x - \frac{1}{y}\right)^2\right\}$$
correct answer:- 1
Question 46
If $$x + \dfrac{1}{x} = 8$$, then find the value of $$\dfrac{5x}{x^2 + 1 - 6x}$$
correct answer:- 2
Question 47
If $$x+y=4$$, $$xy=2$$, $$y+z=5$$, $$yz=3$$, $$z+x=6$$ and $$zx=4$$, then find the value of $$x^3 + y^3 + z^3 — 3xyz$$.
correct answer:- 3
Question 48
If $$p+\dfrac{1}{p}=2$$, find the value of $$p \times p \times p$$
correct answer:- 3
Question 49
If $$x + \dfrac{4}{x} - 4 = 0$$, then the value of $$x^2 - 4$$ is equal to:
correct answer:- 1
Question 50
If $$A = \dfrac{x - 1}{x + 1}$$, then the value of $$A - \dfrac{1}{A}$$ is:
correct answer:- 4
Frequently Asked Questions
These are Quant questions that test how well you can simplify, factor, and evaluate algebraic expressions using basic math rules.
Practice basic algebra rules, focus on like terms, the distributive property, and substitution. Use PDFs and mock tests regularly.
Yes, they form a key part of the Quant section and often appear in both Problem Solving and Data Sufficiency questions.
Students often mix up unlike terms, forget signs, or oversimplify too early. Always check your steps carefully.
Learn standard patterns, use factoring techniques, and avoid unnecessary expansion to save time.
You can download the free PDF with solved questions and formulas from reliable GMAT preparation platforms like GMATPoint
Practicing 15-20 questions daily is enough to build speed and accuracy before the GMAT exam.
Yes, they appear in both Data Sufficiency and Problem Solving, often in age, cost, or work-related problems.