Top 50 – GMAT Quant Sample Questions
Take Free GMAT Daily Targets With Video Solutions
Also, check out the Top 50 – GMAT Quant questions video here:
Question 1: A number X (greater than 0) when increased by 20% yields the same value as that given by a number Y when decreased by 50%. If the difference between Y and X is 140, what is the sum of X and Y?
a) 200
b) 240
c) 300
d) 340
e) 400
1) Answer (D)
Solution:
When X is increased by 20%, we get the value $\frac{\left(100+20\right)}{100}X=1.2X$.
Similarly, when Y is decreased by 50%, we get $\frac{\left(100-50\right)}{100}Y=0.5Y$.
It has been given that 1.2X=0.5Y
or 12X=5Y. -(1)
Also, it has been given that Y-X= 140
Multiplying both sides with 12: 12Y-12X= 12$\times\ $140
12Y-5Y=12$\times\ $140 (from equation (1))
7Y=12$\times\ $140
Y=240
X=100.
Hence, the sum is 340.
Question 2: Two numbers A and B are in the ratio 2:3. 9 is subtracted from both A and B to obtain new values of A and B. Then, 2 is multiplied to the new value of A. The final ratio between A and B thus becomes 10:9. Find the absolute difference between the original values of A and B.
a) 8
b) 9
c) 12
d) 16
e) 24
2) Answer (C)
Solution:
It has been given that the final ratio of A and B is 10:9. Since 2 was multiplied to the new value of A after subtraction, the value of the ratio after subtraction must be 5:9.
Let the original values of A and B be 2k and 3k respectively, where k is the common factor.
Then, we have: $\frac{\left(2k-9\right)}{\left(3k-9\right)}=\frac{5}{9}$
Cross multiplying, we get:
18k-81=15k-45
3k=36
k=12
Thus, the common factor is 12, so the values of A and B are 24 and 36 respectively.
Thus, the absolute difference is 36-12=12.
Question 3: The numbers A and B are in the ratio 1:2. The numbers B and C are in the ratio 6:5. The numbers C and D are in the ratio 10:11. If the sum of these four numbers is 78, find the difference between the largest and the smallest number among them.
a) 11
b) 12
c) 13
d) 14
e) 15
3) Answer (B)
Solution:
It has been given that:
A:B=1:2 and B:C=6:5
Since we can multiply any factor with a ratio, as long as we multiply the factor to both antecedent and consequent:
A:B=3:6 (Multiplying 3)
Since B has the same value in both ratios, we can write: A:B:C=3:6:5.
Similarly multiplying the above ratio with 2: A:B:C=6:12:10.
Also, C:D=10:11
So, we get A:B:C:D=6:12:10:11
Let the common factor be k, so the values of A, B, C, D will be 6k, 12k, 10k, and 11k respectively.
Their sum= 39k = 78 (given)
k=2.
Thus the values of A, B, C, D will be 12, 24, 20, and 22 respectively.
Difference between the largest and the smallest= 24-12= 12.
Question 4: The cost price ‘C’ of an article increased by X%. By what percent should the selling price ‘S’ of the article be increased to maintain the same amount of profit as before?
(1) X=20%
(2) S=2C
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
4) Answer (C)
Solution:
Here, we have three unknowns, the Cost Price, Selling Price, and the Percentage by which the Cost Price increases. Statement (1) tells us about the percentage increase. But since we have no idea what the relative value of CP and SP here is, we cannot comment on the required increase in the SP.
For example, let CP and SP both be 100. Here, profit is zero. Then if CP is raised by 20%, SP should be raised by 20% to get zero profit again.
But if CP=100 and SP= 200, then the profit is 100. If CP increases by 20% to give 120, the SP should be increased by 10% to give 220, so that the profit again becomes 100.
Thus we also need statement (2), which tells us the relative value of CP and SP. If SP=aCP, then an X% increase in CP requires $\frac{X}{a}\%$ increase in SP. Thus the required percentage here will be 10%.
Thus, the answer is (c).
Question 5: A:B::4:13, X:Y::12:17, M:N::19:20. What is the value of A+Y?
(1) A:N::1:5
(2) X:M::12:19
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
5) Answer (E)
Solution:
In the question, we have been given three ratios. Using Statements (1) and (2) we will be able to establish a relation between A and Y. But we will not have a value of A and Y, and will only have the ratio in which these values exist. Thus, we cannot answer the question using both the statements.
Hence, the answer is (e).
⇒ Also checkout: GMAT complete syllabus pdf
⇒ Also, check out the 5 Tips for GMAT preparation
Question 6: Is $a^3+a^2b+2ab^2+b^3$ odd? a and b are natural numbers.
Statement 1: At least one of a and b is odd.
Statement 2: At least one of a and b is even.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
6) Answer (A)
Solution:
$a^3+a^2b+2ab^2+b^3=a^3+3a^2b+3ab^2+b^3-2a^2b-ab^2=\left(a+b\right)^3-ab\left(2a+b\right)$
Now, there are 4 possibilities as follows:
Case 1: a -> odd, b -> odd
Expression = $\left(O+O\right)^3-O\times\ O\left(2O+O\right)=E\ -\ O\times\ O=E-O=O$
Case 2: a -> odd, b -> even
Expression = $\left(O+E\right)^3-O\times\ E\left(2O+E\right)=O\ -\ E\times\ E=O-E=O$
Case 3: a -> even, b -> odd
Expression = $\left(E+O\right)^3-E\times\ O\left(2E+O\right)=O\ -\ E\times\ O=O-E=O$
Case 4: a -> even, b -> even
Expression = $\left(E+E\right)^3-E\times\ E\left(2E+E\right)=E\ -\ E\times\ E=E-E=E$
Only when both of a and b are even, the value is even, at other times, it is odd.
Now, let us examine the two statements:
Statement 1: At least one of a and b is odd. This means Case 1, Case 2, or Case 3. In all these cases we get the value of the given expression as odd. Hence, we can determine using this statement.
Statement 2: At least one of a and b is even. This means Case 2, Case 3 or Case 4. There is no definite answer. It can be odd/ even. Hence, it cannot be determined using this Statement.
Hence, Option (A).
Question 7: The average age of a class of 20 students is 18 years. If two students with an average age of 21 years left the class and three new students with an average age of 27 years joined the class.Which of the following is true regarding average age of the class after three students joined the class.
a) Average age of the class increased by 2 years.
b) Average age of the class decreased by 2 years.
c) Average age of the class increased by 1 year.
d) Average age of the class decreased by 1 year.
e) Average age of the class neither decreased nor increased.
7) Answer (C)
Solution:
It is given that :
The average age of class is 18 years
Now let sum of ages of all students be S
Therefore by averages formula :
18=$\frac{S}{20}$
so S=360
Now 2 students with average age of 21 years left the class
so sum of ages of the two students that left the class : 21*2=42 years
Now 3 students with average age of 27 years joined the class
so sum of ages of the three students that joined the class :27*3=81 years
Therefore the new sum of ages of students present in calss =360-42+81=399
Now number of students in the class =20-2+3=21
Therefore average age = $\frac{399}{21}$=19 years
So the average age increased by 1 year.
Hence option C is the correct answer.
Question 8: A number N = $2^k+5^l+7^m+9^n+11^o$ is divisible by 3. Which of the following is a correct representation of the values of (k,l,m,n,o)?
a) (232, 964, 141, 197, 940)
b) (373, 172, 193, 231, 122)
c) (192, 812, 247, 497, 311)
d) (341, 611, 271, 531, 151)
e) (571, 32, 393, 231, 711)
8) Answer (E)
Solution:
n can take any value, it will always be divisible by 3.
For any value of m, $7^m$ will always leave a remainder of 1 on division with 3.
If we take into account $2^k$, $5^l$, and $11^o$, we can note that for odd values of l, k and o, the remainder in each case is 2, and for the even values it is 1.
Now, the total remainder will be the sum of the remainders in individual cases. Since the total remainder is 0, the sum of all remainders should be zero or divisible by 3.
The remainder of the first term = 1/2
The remainder of the second term = 1/2
The remainder of the third term = 1
The remainder of the fourth term = 0
The remainder of the first term = 1/2
Maximum possible value = 7
Minimum possible value = 4
Hence, it has to be 6 in order to be divisible by 3.
For the value to be 6, two of the first, second and fifth terms must be odd and the remaining term must be even. This is satisfied only in Option E.
Question 9: The first 15 multiples of 5 are separated into three sets X, Y and Z each comprising of 5 numbers. Find the maximum possible sum of medians of three sets.
a) 160
b) 150
c) 165
d) 145
e) 175
9) Answer (B)
Solution:
We have first fifteen multiples of 5 as – 5,10,15,20,25,30,35,40,45,50,55,60,65,70 and 75.
Now we have to divide these in groups of 5 such that each group has maximum possible median.
Now, we know that if n is odd the median of the set is the middle number when numbers are arranged in ascending order.
In this case the middle number will be the 3rd number .
Now therefore we will try to divide numbers such that the 3rd number is maximum possible.
Therefore numbers can be divided among x,y and z as follows:
X={5,10,65,70,75 }
Y={15,20.50,55,60}
Z={25,30,35,40,45}
so the medians of {X,Y,Z} = {65,50,35}
Their maximum sum =65+50+35=150
Question 10: If a natural number N has 24 factors, how many factors will $N^2$ definitely not have?
GMAT Quanta) 135
b) 99
c) 75
d) 70
e) 105
10) Answer (D)
Solution:
If N has 24 factors, then the number of ways it can be represented is
24 = 2 x 2 x 2 x 3 = $abcd^2$ —- $N^2=a^2b^2c^2d^4$
24 = 2 x 3 x 4 = $ab^2c^3$ —- $N^2=a^2b^4c^6$
24 = 2 x 2 x 6 = $abc^5$ —- $N^2=a^2b^2c^{10}$
24 = 4 x 6 = $a^3b^5$ —- $N^2=a^6b^{10}$
24 = 2 x 12 = $ab^{11}$ —- $N^2=a^2b^{22}$
24 = 3 x 8 = $a^2b^7$ —- $N^2=a^4b^{14}$
24 = 24 = $a^{23}$ —- $N^2=a^{46}$
Hence, it can have 135, 105, 99, 77, 75, 69, 47 factors. However, it cannot have 70 factors.
Download GMAT Math Fomrulas PDF
Question 11: X is a set of 5 distinct integers such that its mean is 20. Find the maximum possible integer which can be present in set X if the least integer present is 10.
a) 50
b) 54
c) 56
d) 35
e) 40
11) Answer (B)
Solution:
Now we are given that Mean of integers present in {X} =20
Let integers be a,b,c,d,e and let a be the least integer present in {X}.
Now a=10
Now we know that the 5th integer will be maximum when all the remaining 4 integers will be as less as possible .
Now as all integers are distinct, therefore the 2nd smallest integer will be 10+1=11 , similarly 3rd smallest integer will be 11+1=12 and 4th smallest integer will be 12+1=13.
We know sum of all 5 integers =5*20=100
Therefore maximum possible integer which can be present in set{X}=100-10-11-12-13=54
Hence option B is the correct answer.
Question 12: a and b are two natural numbers(a>b). If s represents a + b, d represents a – b, p represents a x b, then is the sum of s, p and d odd?
Statement 1: a is even
Statement 2: b is odd
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
12) Answer (A)
Solution:
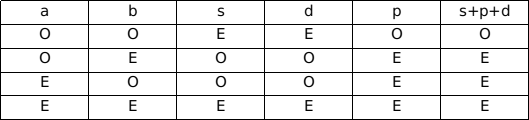
If a is even, the sum of s, p, and d is definitely even.
If b is odd, the sum can be odd or even.
Hence, Option (A) is the correct choice.
Question 13: What is the number of elements in set {S}.
(1) Average of S=8
(2) Standard deviation of S= $\sqrt{\ 10}$
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
13) Answer (E)
Solution:
We are given that
Mean of the data set = 8 and standard deviation =$\sqrt{\ 10}$
We know Mean =$\frac{\left(Sum\ of\ values\ \right)}{Number\ of\ values}$
So we cannot find exact value of N using only mean .
Therefore statement (1) alone is not sufficient.
Similarly using standard deviation only we cannot find the number of values of N.
Now if we use both mean and standard deviation together :
Then also we cannot say exactly how many elements will be present in S as we can have same mean and Standard deviation for two different values of N .
For ex -let us consider set A as A={4,6,8,10,12}
Here average of elements in A = 8 and Standard deviation =$\sqrt{\ 10}$
Now let us consider set B={5,6,9,12}
Here average of elements in B =8 and Standard deviation=$\sqrt{\ 10}$
Therefore Statements (1) and (2) Together also are NOT sufficient.
Hence option (E) is the correct answer.
Question 14: If $a>b^2>\sqrt{c}$, then which of the following might be true?
1. c>a>b
2. a>b>c
3. a>c>b
4. b>a>c
a) Only 1, 2 and 3
b) Only 1, 3 and 4
c) Only 1 and 4
d) Only 2 and 4
e) All four
14) Answer (E)
Solution:
7>6>4 —-> c>a>b
7>6>1 ——> a>b>c
17>10>4 ——–> a>c>b
0.1>0.04>0.02 ——–> b>a>c
Hence, all 4 might be possible.
Question 15: A school is open on all days of the year except on Saturdays and Sundays. In a certain leap year, what is the probability that the school is not open on at least 105 days of the year?
a) 15/52
b) 3/7
c) 5/14
d) 1/2
e) 9/16
15) Answer (B)
Solution:
Any year can start with one of the seven days of the week.
Now, if a year had exactly 52 weeks, it would have 104 holidays. But, since the given year is a leap year, we have an additional 366 – (52 x 7) = 2 days.
If the starting day of the year is Monday, the additional 2 days are Monday and Tuesday.
If the starting day of the year is Tuesday, the additional 2 days are Tuesday and Wednesday.
If the starting day of the year is Wednesday, the additional 2 days are Wednesday and Thursday.
If the starting day of the year is Thursday, the additional 2 days are Thursday and Friday.
If the starting day of the year is Friday, the additional 2 days are Friday and Saturday.
If the starting day of the year is Saturday, the additional 2 days are Saturday and Sunday.
If the starting day of the year is Sunday, the additional 2 days are Sunday and Monday.
Hence, in 3 of the 7 cases, we get 1 or 2 additional Saturdays/Sundays. Hence, the required probability = 3/7.
⇒ Also checkout: GMAT Geometry Formulas pdf
Question 16: If $\alpha$ and $\beta $ are the roots of the equation f(x)=$x^2-8x\ +14$. Find the value of $\alpha\ ^3+\beta\ ^3$
a) 204
b) 162
c) 190
d) 166
e) 176
16) Answer (E)
Solution:
We have equation as $x^2-8x+14=0$
Now $\alpha\ +\beta\ =8$
and $\alpha\ \beta\ =14$
Now $\alpha\ ^3+\beta\ ^3=\left(\alpha\ +\beta\ \right)\left(\alpha\ ^2+\beta\ ^2-\alpha\ \beta\ \right)$
=$\left(\alpha\ +\beta\ \right)\left(\left(\alpha\ +\beta\ \right)^2-2\alpha\ \beta\ -\alpha\ \beta\ \right)$
solving we get :
$\alpha\ ^3+\beta\ ^3 =8(64-42) = 8(22) =176$
Hence option E is the correct answer.
Question 17: A is a set of all vowels and B is a set of all consonants. What is the probability of selecting one alphabet each from A and B such that they are consecutive alphabets?
a) 3/35
b) 2/21
c) 8/105
d) 5/26
e) 1/21
17) Answer (A)
Solution:
Total number of cases = 5 x 21 = 105.
Favourable cases = AB, DE, EF, HI, IJ, NO, OP, TU, UV.
Total = 9.
Hence, probability = 9/105 = 3/35
Question 18: A person has 100 notes of Rs. 10 and Rs. 20 each. He went to a shop and bought items for Rs. 220. In how many ways can he pay this amount using the notes he has?
a) 10
b) 11
c) 12
d) 13
e) 14
18) Answer (C)
Solution:
Let the number of Rs. 10 notes and Rs. 20 notes he uses be ‘x’ and ‘y’ respectively. Then:
10x+20y = 220
x+2y = 22.
We need to find all the combinations of (x,y) for which the equation is satisfied.
If y=0, x=22
y=1, x=20
y=2, x=18
y=3, x=16
y=4, x=14
y=5, x=12
y=6, x=10
y=7, x=8
y=8, x=6
y=9, x=4
y=10, x=2
y=11, x=0
Thus, there are 12 ways he can pay the bill.
Question 19: A person has a fixed amount of pocket money, all of which she spends on chocolates and toffees. From the amount she gets, she buys 10 chocolates and 20 toffees. Sometimes she also buys 6 chocolates and 40 toffees. Due to some reason, the pocket money she received got reduced by 40%. What is the maximum number of toffees she can buy now, given she buys atleast 1 chocolate.
a) 36
b) 37
c) 43
d) 45
e) 50
19) Answer (B)
Solution:
It has been given that she exhausts the total amount on chocolate and toffees. Let the cost of 1 chocolate be C and that of 1 toffee be T.
Pocket money = 10C+20T = 6C+40T.
Solving, we get 4C=20T or C=5T.
Let the cost of 1 toffee be Rs. 1. Then that of the chocolate = Rs. 5.
Total pocket money = $10\times5+20\times1=70$.
Since the pocket money got reduced by 40%, the new pocket money = $\frac{\left(100-40\right)}{100}\times70=42$.
To maximise the number of toffees that can be bought, we minimize the number of chocolates bought.
At least 1 chocolate has to be bought. So money left for toffees = 42-5 = 37.
Thus, the number of toffees that can be bought = $\frac{37}{1}$= 37
Question 20: The price of a wooden log increases with the length linearly. A long wooden block is chopped off along its cross-section into three pieces of length in the ratio 1:2:3. Because of this, the total price increased by Rs. 30. If the price of the original log was Rs. 45 more than the price of the new smallest log, find the price of the new largest log.
a) 14
b) 18
c) 36
d) 42
e) 54
20) Answer (D)
Solution:
Let the length of the original log be 6x. Then the lengths of the new logs will be x, 2x, and 3x.
Since the price varies linearly, it should be of the form:
Price=al+b, where a and b are constants and l is the length of the log.
As given: a(6x)+b + 30 = a(x)+b + a(2x)+b + a(3x)+b
We get b=15.
Also, it has been given that a(6x)+b – 45 = a(x)+b
5ax = 45
ax= 9.
The price of the new largest log = 3ax+b = 27 + 15 = 42.
Take Free GMAT Daily Targets With Video Solutions
Question 21: Rachel goes to the gym either in the morning or in the evening. For how many days, in a period of X days, did she not go to the gym at all, that is neither in the morning nor in the evening?
(1) X=31 days.
(2) She was in the gym on 14 mornings and was not in the gym for 15 evenings.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
21) Answer (B)
Solution:
Let the number of days she visited in the evening be ‘a’ and the number of days she did not visit the gym in the morning be ‘b’. The total number of evenings will be equal to the total number of mornings over the period of X days.
From (2), we can see that she went to the gym for 14 mornings. This means that there would be 14 days when she went in the morning but did not go in the evening.
But it has also been given that there are 15 evenings where she did not visit the gym. This means that there was 1 evening, where she did not visit in the evening as well as the morning. Thus, she did not visit the gym on 1 day. (2) is sufficient.
(1) only tells us the time period and nothing else. Hence, it is not sufficient.
Hence, the answer is (b).
Question 22: The ages of a father and a son are in the ratio 13:7. After how many years will the son be as old as his father is now?
(1) The difference between their ages is a natural number that lies between 10 and 20.
(2) Three years ago, the father’s age was twice that of his son.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
22) Answer (B)
Solution:
Let the father’s present age be 13x and that of the son be 7x.
Then their ages 3 years ago: 13x-3 and 7x-3.
From (2), we have 13x-3=2$\times\ $(7x-3)
13x-3=14x-6
x=3.
Hence the ages of the father and the son are 36 and 21, and the son would be of age 36 after 15 years. Hence (2) is sufficient.
From (1), we have two cases: The ages of (father, son) can be (26,14) or (39,21), as they satisfy the ratio and the difference also lies between 10 and 20. Hence, (1) is not sufficient.
Hence, the answer is (b).
Question 23: Is the probability of getting ‘one’ more than the probability of getting ‘two’ in a single roll of a biased dice?
Statement 1: The probability of getting a prime number is the same as the probability of not getting an even number.
Statement 2: The probability of getting a prime number is the same as the probability of not getting an odd number.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
23) Answer (A)
Solution:
The probability of getting a prime number is equal to the sum of probabilities of getting the individual prime numbers.
P(prime) = P(2) + P(3) + P(5)
Similarly, P(not even) = P(odd) = P(3) + P(5) + P(1)
Also, P(not odd) = P(even) = P(2) + P(4) + P(6)
Statement 1: P(2) + P(3) + P(5) = P(3) + P(5) + P(1) => P(2) = P(1)
Statement 2: P(2) + P(3) + P(5) = P(2) + P(4) + P(6) => P(3) + P (5) = P(4) + P(6)
Hence, Statement 1 alone is sufficient, but Statement 2 alone is not sufficient.
Question 24: In how many permutations of the word VACCINE do no two vowels come together?
a) 360
b) 720
c) 648
d) 324
e) 576
24) Answer (B)
Solution:
We can place the vowels as shown:
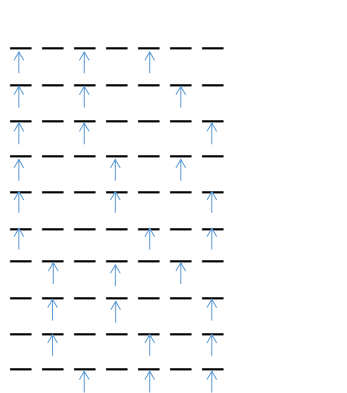
Now, there are a total of 10 cases.
In each case, we can arrange the 3 different vowels in 3! ways and the 4 consonants in 4!/2! ways. Hence, each case further contributes to 72 different ways.
Hence, 72 x 10 = 720.
Question 25: The final match of the World Test Championship can have the following results: Team India wins, Team New Zealand wins, a draw. What is the probability that India wins?
Statement 1: The probability that New Zealand wins is 0.4
Statement 2: The probability that one of the teams will definitely win is 0.812
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
25) Answer (C)
Solution:
P(I) + P(NZ) + P(Draw) = 1
Statement 1: P(NZ) = 0.4
Statement 2: P(I) + P(NZ) = 0.812
Hence, from both statements, we can find out P(I). HENCE, Option C.
⇒ Also checkout: GMAT Arithmetic Formulas pdf
Download GMAT Math Fomrulas PDF
Question 26: F(x) is a quadratic equation having value 4 at x=0 . The minimum value of F(x) occurs at x=2. Find the value of F(8) if the minimum value of F(x) is 0.
a) 18
b) 42
c) 36
d) 30
e) 24
26) Answer (C)
Solution:
Let F(x) be $ax^2+bx+c=0$
Now F(0)=4
⇒ a(0)+b(0)+c=4
⇒ c=4
Now we know that minimum value of a quadratic equation occurs at x=$-\frac{b}{2a}$
Therefore $-\frac{b}{2a}=2$
or 4a+b=0 (1)
We also know that F(2)=0
so we get 4a+2b+4=0 (2)
Solving (1) and (2) we get
a=1 and b=-4
Therefore f(x)=$x^2-4x+4$
Now F(8)=36
Question 27: Find the number of integral values of $x$ for which $|x^2-8x+15| < 3$
a) 3
b) 1
c) 6
d) 5
e) 2
27) Answer (A)
Solution:
We have f(x) as$\left|x^2-8x+15\right|$
Now we know that |x|=x if x>=0 and |x|=-x if x<0
$\left|x^2-8x+15\right|$= $x^2-8x+15$
if $x^2-8x+15\ge0$
(x-5)(x-3)$\ge0$
x$\ge5$ or x$\le3$ (1)
Now x^2-8x+15<3
x^2-8x+12<0
(x-6)(x-2)<0
so x ∈(2,6)
From (1) x cannot be 4
so x can be 3 and 5.
Now $\left|x^2-8x+15\right|=-x^2+8x-15\ $
when x^2-8x+15<0
x∈(3,5) (2)
Now solving we get
–x^2+8x-15<3
x^2-8x+18>0
Now 8^2-4*18=-8 which is <0 and coefficient of x^2>0
Therefore x^2-8x+18 will be positive for all x
So integral solution will be x=4.(From (2) )
Therefore total integral solutions will be 3.( 3,4 and 5)
Question 28: Find the number of distinct roots of the equation F(x)=$x^3-8x^2+21x-18=0$
a) 0
b) 1
c) 2
d) 3
e) None of the above .
28) Answer (C)
Solution:
We have f(x)=$x^3-8x^2+21x-18=0$
Now by observation we can say f(2)=0
Therefore 2 is a root of the equation
Now Therefore F((x)= (x-2)(x^2-6x+9)
Now we have to factorize (x^2-6x+9)
(x^2-6x+9)=(x-3)^2
Therefore F(x)=(x-2)(x-3)^2
So the roots of F(x) are 2,3,3
Therefore distinct roots = 2.
Question 29: F(x)= $ax^2+bx+c=0$ is a quadratic equation with roots p and q. Are p and q equal ?
Statement 1: c is a perfect square.
Statement 2: The discriminant of F(x)=0 is zero.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
29) Answer (B)
Solution:
We have f(x)=$ax^2+bx+c=0$
Now we know that if the Discriminant of a quadratic equation equals 0, the roots of the equation are equal .
Hence Statement 2 alone is sufficient .
Now statement 1 says c is a perfect square , now we know that c is the product of roots
now it is possible the product of any two distinct numbers also result in a perfect square (For example 27*3=81 which is a perfect square )
and product of two equal numbers also result in a perfect square (9*9=81)
Therefore we can say Statement (1) alone is not sufficient.
Therefore option B is the correct answer.
Question 30: In a car showroom 60 cars are placed in line where the positions are numbered from 1 to 60 based on their place of allocation. Three people Arjun, Bhavan and Charan come for buying the cars. Arjun wants to buy all the cars that are placed in positions which are multiples of 3. Bhavan wants to buy the cars which are placed in positions which are multiples of 4. Charan wants to buy the cars which are placed in positions which are multiples of 5. How many cars does exactly two people want to buy ?
a) 8
b) 9
c) 10
d) 11
e) 12
30) Answer (B)
Solution:
Assuming the cars Arjun want to buy to be A.
Assuming the cars Bhavan wants to buy to be B.
Assuming the cars Charan wants to buy to be C.
The question asks for the cars which exactly two people want to buy.
This is given by :
N(A∩B) +N(B∩C) +N(C∩A)- N(A∩B∩C)
N(A) = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60)
N(B) = (4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60)
N(C) = (5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60).
N(A∩B)= (12, 24, 36, 48, 60) = 5
N(B∩C)= (20, 40, 60) = 3
N(C∩A) = (15, 30, 45, 60) = 4
N(A∩B∩C)= (60) = 1 ( Which is included for Arjun, Bhavan, Charan). Hence the 1*3 = 3
N(A∩B) +N(B∩C) +N(C∩A)- N(A∩B∩C) = 5+4+3-3 = 9.
Take Free GMAT Daily Targets With Video Solutions
Question 31: Is x/y > 1? x and y are positive real numbers.
Statement 1: xy<1
Statement 2:y<1
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
31) Answer (E)
Solution:
Is x/y > 1?
Since y>0, we can denote it as
is x>y? Hence, we need to figure out if x > y.
Statement 1: xy<1, now there might be three possibilities.
1. x < 1, y < 1
2. x>=1, y< 1
3. x < 1, y>= 1
Statement 2: y < 1. Hence, we are still left with 1 and 2.
Now, in case 2, we definitely know that x>y, however in case 1, we cannot determine the same. Hence, option E.
Question 32: How many integer values of x exist such that $\frac{\left(x^2-6x+8\right)}{\left(x^2+3x-54\right)}<0$?
a) 0
b) 5
c) 9
d) 10
e) 11
32) Answer (E)
Solution:
$\frac{\left(x^2-6x+8\right)}{\left(x^2+3x-54\right)}<0$
By factorizing the expressions in both numerator and the denominator, we get:
$\frac{\left(x-2\right)\left(x-4\right)}{\left(x-6\right)\left(x+9\right)}<0$
Thus we have four determining points, -9, 2, 4, 6.
The expression will be negative when x lies between (-9,2) where (x+9) term will be positive and the other three will be negative, and (4,6) where (x-6) will be negative and the other 3 are positive.
Hence we have 11 values: -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, and 5.
Question 33: For the school athletic meet a student must enroll either in sports or in voluntary activities. Soccer, Basketball and Tennis are the sports which a student can enroll. If the students who enrolled only for Soccer = 25% of the total students.If the students who enrolled only for basketball = 19% of the total students.If the students who enrolled only for Tennis = 20% of the total students.If the percentage of students who enrolled for all the three sports is equal to 12 percent of total students and 6 percent of the total students enrolled for exactly two of the three sports. What is the percentage of students who enrolled for volunteering ?
a) 12%
b) 14%
c) 16%
d) 18%
e) 20%
33) Answer (D)
Solution:
Assuming the students enrolled for soccer only to be A
Assuming the students enrolled for basketball only to be B
Assuming the students enrolled for Tennis only to be C
Assuming the students enrolled for volunteering to be D
N(AUBUC) + N(D) = 100%
N(A)= 25%, N(B)= 19%, N(C)= 20%,
N(A∩B) +N(B∩C) +N(C∩A)= 12%, N(A∩B∩C)= 6%
N(AUBUC)= Percentage of people who play exactly one sport+percentage of people who play exactly two sports + percentage of people who play exactly three sports.
= (25%+19%+20%+12%+6%)
= 82%
N(D) = 100%- 82%
= 18%
Question 34: How many real solutions does the equation f(x)=$x^2+px+q=0$ have ?
Statement 1: $p^2>8q$
Statement 2: q is a perfect cube.
a) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient.
e) Statements (1) and (2) TOGETHER are NOT sufficient.
34) Answer (A)
Solution:
We have f(x)=$x^2+px+q=0$
Now discriminant =$p^2-4q$
We know that if Discriminant >0
the number of real roots =2 of any quadratic equation
and as statement 1 say p^2>8q so this means p^2>4q hence discriminant >0
So Statement (1) ALONE is sufficient.
Now Statement (2) says q is a perfect cube
from this we cannot infer that whether p^2>4q if q is a perfect cube
Therefore statement (2) alone is not sufficient
Hence option A is the correct answer.
Question 35: f(x) is a function defined as f(x)= $x(x-11)$. g(x) is another function, defined as g(x)= $-2x^2+11x\ -7$. For which of the following values of x is f(x)=g(x)?
a) 3
b) 5
c) 6
d) 7
e) 11
35) Answer (D)
Solution:
Given: f(x)=g(x)
Or $x^2-11x=-2x^2+11x-7$
$3x^2-22x+7=0$
$3x^2-21x-x+7=0$
$\left(3x-1\right)\left(x-7\right)=0$
Thus x=$\frac{1}{3}$ or x=7.
Only x=7 is given in the options, hence, the answer is (d).
⇒ Also checkout: GMAT Profit & Loss Formulas pdf
Question 36: If f(x) = 2x + 7 and g(x) = f(1/x), find out the number of integral values of x, where |x| <= 50, such that f(x) >= g(x)
a) 25
b) 50
c) 51
d) 52
e) 78
36) Answer (C)
Solution:
f(x) >= f(1/x)
2x + 7 >= 2/x + 7
2x >= 2/x
x >= 1/x
Let x > 0.
$x^2$ >= 1.
Hence, x >= 1.
Let x < 0.
$x^2$ <=1
Hence, -1<=x<0
Hence, all values of x are {-1, 1, 2, 3, 4, 5, 6, 7, …….., 50} = 51.
Question 37: In a class, a student can opt to study one elective among Science or Maths. A student can also opt to study both the electives or none of them. A total of 120 students were in the class. The number of students who opted for Science is 52. If the number of students who opted for only Maths is 42. If
P = Number of students who opted only for Science.
Q = Number of students who opted for both Science and Maths
Given that P >10, Q > 10. How many ordered pairs of (P, Q) are possible?
a) 25
b) 26
c) 28
d) 30
e) 31
37) Answer (E)
Solution:
Assuming the students who opted only for Science to be A.
Assuming the students who opted only for Maths to be B.
Assuming the students opted for both Maths and Science to be C
Assuming the students opted for none among Maths and Science to be D.
Given in the question N(A)+N(C) = 52
N(B) = 42
The total number of students in the class = 120.
N(A)+N(B)+ N(C)+N(D) = 120.
Let N(D) = k
= 52+42+k = 120
= k = 26.
N(D) = 26.
Given N(A)+N(C) = 52, N(A)>10, N(C)>10.
As per the Question we were informed.
Number of students who opted only for Science = P. Hence (A = P)
Number of students who opted for both Science and Maths = Q. (C= Q)
N(P)= 10+x, N(Q)= 10+y.
10+x+10+y = 52.
x+y = 32
x, y can take only positive values less than 32.
So x, y will have 31 possibilities from 1 to 31.
(P, Q) = (11,41), (12, 40), ……………………… (41, 11)
A total of 31 possibilities.
Question 38: If a venn diagram formed using two elements X, Y. What is N(XUY) ?
Statement 1 : N(Y)+ N(X∩Y) = 22
Statement 2 : N(X)+ N(X∩Y) = 14.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient.
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient.
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
38) Answer (E)
Solution:
N(XUY) = N(X)+ N(Y)-N(X∩Y).
As per the given statements we need the sum of
N(Y)+ N(X∩Y) +(N(X)) or
N(X)+ N(X∩Y)+ (N(Y)).
Hence we cannot find the solution either statement 1 or 2 alone to find the result
Using both the conditions simultaneously gives :
if assumed N(Y) = a, N(X∩Y) = 22-a. As per the second condition if N(X∩Y) = 22-a. N(Y) = a-8.
Hence we cannot find an answer after combining both the statements also.
Question 39: $S_n$ is a series, where every nth term $T_n$ (n>1) is obtained by multiplying the (n-1)th term by a constant r. Is $T_{37}$ greater than $T_{24}$? It is given: |r| > 1
Statement 1: The product of the first term and r is positive.
Statement 2: The 49th term of the series is negative.
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
39) Answer (B)
Solution:
Considering Statement 2, a is negative.
Now, $T_{37}=\frac{a\left(r^{37}-1\right)}{r-1}$
Now, r has an absolute value of greater than 1.
So, it is a large negative number.
$T_{24}=\frac{a\left(r^{24}-1\right)}{r-1}$
If r is positive, the sum is negative but not as low as the previous sum, if r is negative, the sum is always positive.
Hence, 2 is sufficient
Statement 1 only states that either both a and r are positive or both are negative.
This is not sufficient to decide which of the two sums is higher.
Hence, Statement 1 is not sufficient.
Option (B).
Question 40: In a book club meeting a total of 95 students attended the meeting this includes people who study fiction, non fiction, both of them or none of the above two.The number of students who study only fiction to students who only study non fiction is 10 : 7.What is the number of students who study both fiction and non fiction ?
Statement 1: The sum of the number of students who only study non fiction and the students who do not study both fiction and non fiction = 52. The number of students who do not study both fiction and non fiction is 24.
Statement 2 : The sum of number of students who only study fiction and students who only study non fiction is 68
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient.
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient.
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
40) Answer (A)
Solution:
Assuming the number of students who study only fiction = N(A)
Assuming the number of students who study only only fiction = N(B)
Assuming the number of students who do not study both fiction and non fiction = N(C)
Given in the question N(A) : 10k, N(B) = 7k.
N(A)+N(B)+N(A∩B)+N(C) = 95.
17k++N(A∩B)+N(C) = 95.
Using statement 1 : We have :
7k+24 = 52.
K = 4.
17k+N(A∩B)+N(C) = 95.
68+N(A∩B)+24 = 95
N(A∩B) = 3
Using statement 2 :
17k = 68. k =4 is the only thing we can find.
Take Free GMAT Daily Targets With Video Solutions
Question 41: h(x) = sum of digits of x, if the highest factor of x(other than x itself) is even
h(x) = product of digits of x, otherwise
Which of the following represents the correct order of values of h(49), h(90), h(120), h(76) and h(19)?
a) h(49) > h(76) > h(19) > h(120) > h(90)
b) h(49) > h(19) > h(76) > h(120) > h(90)
c) h(49) > h(19) > h(76) > h(90) > h(120)
d) h(49) > h(19) > h(90) > h(76) > h(120)
e) h(19) > h(49) > h(76) > h(90) > h(120)
41) Answer (A)
Solution:
h(49) = 36
h(90) = 0
h(120) = 3
h(76) = 13
h(19) = 9
Hence, option A is right.
Question 42: If $\left(\frac{1}{6}\right)^x\cdot\left(\frac{1}{10}\right)^{y\ }$ is rewritten as : $\left(\frac{1}{2}\right)^z\cdot\left(\frac{1}{3}\right)^x\left(\frac{1}{15625}\right)$. Given x-y = 2. If z is given by x+y. What is the z ?
a) 12
b) 14
c) 16
d) 18
e) 20
42) Answer (B)
Solution:
If $\left(\frac{1}{6}\right)^x\cdot\left(\frac{1}{10}\right)^{y\ }$ = $\left(\frac{1}{2}\right)^{x+y}\cdot\left(\frac{1}{3}\right)^x\cdot\left(\frac{1}{5}\right)^y$.
It was rewritten as per the question :
= $\left(\frac{1}{2}\right)^z\cdot\left(\frac{1}{3}\right)^x\left(\frac{1}{15625}\right)$.
= $\left(\frac{1}{15625}\right)\ =\ \left(\frac{1}{5}\right)^6$.
= $\left(\frac{1}{2}\right)^z\left(\frac{1}{3}\right)^x\left(\frac{1}{5}\right)^6$.
Since z is given by x+y as per the question.
= $\left(\frac{1}{2}\right)^{x+y}\left(\frac{1}{3}\right)^x\left(\frac{1}{5}\right)^6$ = $\left(\frac{1}{2}\right)^z\cdot\left(\frac{1}{3}\right)^x\left(\frac{1}{15625}\right)$
Since the value of x-y is 2.
x = 8.
z = x+y
= 8+6 =14
Question 43: f(x) is a function such that f(x+1)-f(x)=x . Find the sum of all values of f(x) when x varies from 1 to 6 if it is known that f(5)=24.
a) 169
b) 84
c) 124
d) 119
e) 100
43) Answer (D)
Solution:
F(x+1)-F(x)=x
so F(6)-F(5)=5
so F(6)=24+5=29
Similarly F(5)-F(4)=4
so F(4)=20
Similarly F(3)=17 , F(2)=15 and F(1)=14
Now sum of values of F(1) to F(6) =14+15+17+20+24+29
=119
Question 44: $\frac{\left(3^{26}-3^{22}\right)}{4}$ is less than which of the following options ?
a) $3^{24}$
b) $3^{20}+3^{22}$
c) $3^{26}-3^{24}$
d) $3^{20}+3^{22}+\ 3^{23}$
e) $3^{25}-3^{24}$
44) Answer (C)
Solution:
The value $\frac{\left(3^{26}-3^{22}\right)}{4}$ can be re written as :
$\frac{\left(3^{22}\right)\left(3^4-1\right)}{4}$ = $3^{22}\left(20\right)$.
= Option 1 can be rewritten as :
$3^{22}\left(9\right)$. This is less than the value in question.
Option 2 can be rewritten as :
$3^{20}\left(10\right)$. This is less than the given value.
Option 3 can be rewritten as :
$3^{24}\left(8\right)\ =\ 3^{22}\left(72\right)$. Greater than the given value.
Option 4 can be rewritten as :
$3^{20}\left(1+9+26\right)\ =\ 3^{22}\left(\frac{37}{9}\right)$. Lesser value
Option 5 can be rewritten as :
$3^{24}\left(2\right)\ =\ 3^{22}\left(18\right)$. Lesser value
Question 45: Arrange the following numbers on the basis of decreasing order.
1)$2^{120}$
2) $3^{86}$
3) $6^{35}$
a) 2, 1, 3
b) 2, 3, 1
c) 1,2, 3
d) 1, 3, 2
e) 3, 1, 2
45) Answer (A)
Solution:
Comparing 1 and 2.
$\left(2^3\right)<\left(3\right)^2$.
Raising the powers by 40 for the values :
We get : $2^{120}<\ 3^{80}$
$\ 3^{80}\ <\ 3^{86}$.
Comparing 2 and 3.
3 can be re written as :$\left(2\right)^{35}\cdot\left(3\right)^{35}$.
Cancelling the common powers of 3 we are left with $2^{35\ }and\ 3^{51}$.
$2^{35\ }is\ less\ than\ 3^{51}$.
2 is greater than 3
Comparing 1 and 3 :
3 can be re written as :$\left(2\right)^{35}\cdot\left(3\right)^{35}$.
Cancelling the common powers of 2 we are left with :
$2^{120}$ = $2^{85}$
$6^{35}$ = $3^{35}$.
Comparing$2^{85\ }and\ 3^{35}$
$2^4>\ 3^2$
Raising the powers by 20 we get :
$\left(2^4\right)^{20}>\ \left(3^2\right)^{20}$
$2^{80}>\ 3^{40}$
Hence $2^{85}>\ 3^{35}$
1 is greater than 3.
Hence 2>1>3
⇒ Also checkout: GMAT Ratio & Proportion Formulas pdf
Download GMAT Math Fomrulas PDF
Question 46: If given that x,y,z are integers. What is the sign of y ?
Statement 1 : $x^2+y^2-z^2<0$
Statement 2 : x+y > z
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient.
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient.
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
46) Answer (E)
Solution:
As per statement 1 :
$x^2+y^2-z^2<0$ can be written as
$x^2+y^2<z^2$. (1)
y can either be positive or negative.
Going by the second statement.
x+y>z. (2)
We cannot determine the sign from this.
Squaring equation 2 we can either have
$x^2+y^2+2*xy>\ z^2$
$x^2+y^2+2*xy<\ z^2$
Based on the magnitude of x+y, z
Hence we cannot uniquely determine the sign of either x, y or z.
Question 47: If two of the sides of a triangle are 7, 5. How many obtuse angled triangles are possible with all three integral sides ?
a) 1
b) 2
c) 3
d) 4
e) 5
47) Answer (E)
Solution:
If a,b,c are the sides of a triangle.
The conditions are a+b>c, b+c>a, c+a>b
a-c<b, b-c<a, c-a<b
Given that 8, 6 are two sides the third is less than 7+5 = 12.
Similarly greater than > 7-5
= 2.
Hence the third side could be 3, 4, 5, 6, 7, 8, 9, 10, 11,
(3,5,7), (4,5,7), (5,5,7), (6,5,7), (7,5,7), (8,5,7), (9,5,7) (10,5,7) (11,5,7)
The condition for obtuse angled triangle is
$a^2+b^2<\ c^2$
This is possible for (3,5,7), (4,5,7), (9,5,7), (10,5,7), (11,5,7)
Hence 5 are possible
Question 48: The standard deviation of a set of n values is 41 and the mean of the same set of values is 36. A number a is being added to this set of numbers. Will it increase the standard deviation of this set of numbers?
Statement 1: |x|<5
Statement 2: x is non-negative
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
48) Answer (A)
Solution:
For any set of numbers, if we add a number to the set, the standard deviation increases if |N – mean| > Standard deviation. Here, N is the number that is to be added.
Now, we need to check if
|N – 36| > 41
or
N – 36 < -41 or N – 36 > 41
N < -5 or N > 77
The first statement definitely states that N is not < -5. Hence, it is sufficient to answer the question.
Option (A) is correct.
Question 49: Is $x^2$ > x|x| ?
Statement 1: $x^3+x^2<0$
Statement 2: $x^2$ is not equal to -x|x|
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
49) Answer (D)
Solution:
The above condition is only satisfied when x < 0.
Statement 1: $x^3+x^2<0$
$x^3+x^2<0\ ->x^2\left(x+1\right)<0\ ->x<-1$ x is negative. Hence this is sufficient.
Statement 2: $x^2$ is not equal to -x|x|
If x < 0, $x^2$ is equal to -x|x|. Since this condition is not being satisfied, we can say that x is not < 0. Hence, this is also sufficient.
Hence, option D
Question 50: Is $a^a+b^b+c^c+d^d$ odd? a, b, c and d are different natural numbers.
Statement 1: a x b x c x d is odd
Statement 2: a x b is odd and c x d is even
a) Statement (1) ALONE is sufficient, but Statement (2) alone is not sufficient
b) Statement (2) ALONE is sufficient, but Statement (1) alone is not sufficient
c) Both Statements (1) and (2) TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d) EACH statement ALONE is sufficient
e) Statements (1) and (2) TOGETHER are NOT sufficient
50) Answer (A)
Solution:
An odd number raised to any number is always od and vice versa. Hence the powers do not matter.
So, we need to find out if
a + b + c + d is odd
This is possible if one of them or three of them are odd.
Now, let us consider the statements.
Statement 1: abcd is odd only when all of them are odd. Hence this sufficiently tells us that a + b + c + d is not odd.
Statement 2: ab is odd, cd is even -> a and b are mandatorily odd; out of c and d, at least one should be even. Hence, this does not lead us to a definitive conclusion.
Hence, Option (a) is right.
These GMAT quant practice questions have the video solutions.
You have downloaded geometry formulas for GMAT we also refer to our other pdf like GMAT Arithmetic formulas PDF
Check out the complete GMAT syllabus and Section-wise Preparation Tips
Check out the PDFs for Ratio & Proportion Formulas, Profit and Loss Formulas.
Join GMATPOINT Telegram Channel
If you are starting your GMAT preparation from scratch, you should definitely check out the GMATPOINT
