GMAT Algebraic Expressions Questions With Solutions, Download PDF

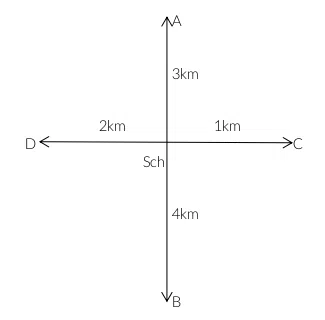
From the information, D is in the west, B is in the south, C is in the east and A is in the north. Also, B is 4km from the school. A is not at 1km from the school. From the information given in this question, A is located at 3km from the school. Since C’s playground is closer to the school than D’s, C should be at 1km and D should be at 2km from the school. Since D is located in the west, the playground located in the west is at a distance of 2km from the school.

Expression : $$\frac{p^2}{q^2}+\frac{q^2}{p^2}$$ = 1

=> $$\frac{p^{4}+q^{4}}{p^2q^2}$$ = 1

=> $$p^4+q^4 = p^2q^2$$ --------------Eqn(1)

Now, to find : $$(p^{6}+q^{6})$$

=> $$(p^2)^3 + (q^2)^3$$

Using the formula, $$a^3 + b^3 = (a+b)(a^2+b^2-ab)$$

=> $$(p^2+q^2)(p^4+q^4-p^2q^2)$$

From eqn (1), we get :

=> $$(p^2+q^2)(p^2q^2-p^2q^2)$$

=> $$(p^2+q^2)*0$$

= 0

Using the formula, $$(x-y)^3 = x^3 - y^3 -3xy(x-y)$$

=> $$(m - 5n)^3 = m^3 - 125n^3 - 15mn(m-5n)$$

=> $$2^3 = m^3 - 125n^3 - 15mn*2$$

=> $$m^3 - 125n^3 - 30mn = 8$$

$$\sqrt{7 + 4\sqrt{3}} = \sqrt{7 + 2*2*\sqrt{3}}$$

= $$\sqrt{4 + 3 + 2*2*\sqrt{3}} = \sqrt{(2 + \sqrt{3})^2}$$

= $$2 + \sqrt{3}$$

Expression : $$\frac{4+3\sqrt{3}}{2 + \sqrt{3}}= A+\sqrt{B}$$

=> $$\frac{4 + 3\sqrt{3}}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}} = A + \sqrt{B}$$

=> $$\frac{8 - 4\sqrt{3} + 6\sqrt{3} - 9}{4 - 3} = A + \sqrt{B}$$

=> $$2\sqrt{3} - 1 = A + \sqrt{B}$$

=> $$A = -1$$ and $$\sqrt{B} = 2\sqrt{3}$$

=> $$B = (2\sqrt{3})^2 = 12$$

=> $$B - A = 12 - (-1) = 13$$

Expression : $$a^{2}+1=a$$

=> $$a^2 - a + 1 = 0$$

Multiplying by $$(a+1)$$ on both sides

=> $$(a+1)(a^2-a+1) = 0$$

=> $$a^3 + 1^3 = 0$$

=> $$a^3 = -1$$

To find : $$a^{12}+a^{6}+1$$

= $$(a^3)^4 + (a^3)^2 + 1$$

= $$(-1)^4 + (-1)^2 + 1$$

= $$1+1+1 = 3$$

Expression : $$p- 2q = 4$$

Cubing both sides, we get :

=> $$(p - 2q)^3 = 4^3$$

=> $$p^3 - 8q^3 - 6pq(p - 2q) = 64$$

=> $$p^3 - 8q^3 - 24pq = 64$$

=> $$p^3 - 8q^3 - 24pq - 64 = 0$$

$$(x^2+\frac{1}{x^2})$$ = $$(x + \frac{1}{x})^2$$ - 2

and

$$(x^3 + (\frac{1}{x})^3)$$ = $$(x + \frac{1}{x})$$ ($$(x + 1/$$(x)$$)^2$$ -3)

so the value of

$$(x^2+\frac{1}{x^2})(x^3+\frac{1}{x^3})$$ = (4-2)(2 (4-3)) = 4

$$a^{3} + b^{3} + c^{3} - 3abc$$ = (a+b+c)($$(a^2 + b^2 + c^2)$$ - ab -bc-ac)

we will get minimum value when a=b=c as all are positive so the minimum value is 0

$$a=\frac{2+\sqrt{3}}{2-\sqrt{3}}$$ on rationalising we will get a = $$(2 + \surd3)^2$$

$$b=\frac{2-\sqrt{3}}{2+\sqrt{3}}$$ on rationalizing we will get b = $$(2 - \surd3)^2$$

now putting values of a and b in , $$a^2+b^2+a \times b$$

$$a^2+b^2+a \times b$$ = 195

given that a + b + 1 = 0

we know if a+b+c = 0

then $$a^3 + b^3 + c^3 - 3abc$$ = 0

as we can see that $$(a^3 + b^3 +1 - 3ab)$$ resembles $$a^3 + b^3 + c^3 - 3abc$$ with c = 1

and hence $$(a^3 + b^3 +1^3 - (3ab \times 1))$$ = 0

Expression : $$\frac{3-5x}{x} + \frac{3-5y}{y} + \frac{3-5z}{z} = 0 $$

=> $$\frac{3}{x} - \frac{5x}{x} + \frac{3}{y} - \frac{5y}{y} + \frac{3}{z} - \frac{5z}{z} = 0$$

=> $$\frac{3}{x} + \frac{3}{y} + \frac{3}{z} - 15 = 0$$

=> $$3 (\frac{1}{x} + \frac{1}{y} + \frac{1}{z}) = 15$$

=> $$\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{15}{3} = 5$$

Using the rule, $$a^2 - 2ab + b^2 = (a-b)^2$$

=> $$16a^2 - 12a = (4a)^2 - 2*4a*\frac{3}{2}$$

= $$(4a)^2 - 2*4a*\frac{3}{2} + (\frac{3}{2})^2 - \frac{9}{4}$$

= $$(4a - \frac{3}{2})^2$$

=> $$\frac{9}{4}$$ should be added to make the above expression a perfect square.

A quadratic equation : $$ax^2 + bx + c = 0$$ has equal roots iff Discriminant, $$D = b^2 - 4ac = 0$$

(A) : $$x^2 + 14x - 49 = 0$$

=> D = $$(14)^2 - 4(1)(-49) = 196 + 196 = 392 \neq 0$$

(B) : $$x^2 + 7x + 49 = 0$$

=> D = $$(7)^2 - 4(1)(49) = 49 - 196 = -147 \neq 0$$

(C) : $$x^2 - 7x - 49 = 0$$

=> D = $$(-7)^2 - 4(1)(-49) = 49 + 196 = 245 \neq 0$$

(D) : $$x^2 + 14x + 49 = 0$$

=> D = $$(14)^2 - 4(1)(49) = 196 - 196 = 0$$

Thus, the equation : $$x^2 + 14x + 49 = 0$$ has equal roots.

Expression : $$\frac{(b^{3}x^{2}a^{4}z^{3})\times(b^{4}x^{3}a^{3}z^{2})}{(a^{2}b^{4}z^{3})}$$

= $$(a)^{4 + 3 - 2} \times (b)^{3 + 4 - 4} \times (x)^{2 + 3} \times (z)^{3 + 2 - 3}$$

= $$(a)^5 (b)^3 (x)^5 (z)^2$$

=> Ans - (C)

Equation 1 : $$a + b = 10$$

=> $$a = 10 - b$$

Equation 2 : $$a \times b = 24$$

Substituting value of 'a' in equation 2, we get :

=> $$(10 - b) b = 24$$

=> $$10b - b^2 = 24$$

=> $$b^2 - 10b + 24 = 0$$

=> $$b^2 - 4b - 6b + 24 = 0$$

=> $$b(b - 4) - 6(b - 4) = 0$$

=> $$(b - 4) (b - 6) = 0$$

=> $$b = 4 , 6$$

=> $$a = 6 , 4$$

$$\therefore a^3 + b^3 = (4)^3 + (6)^3$$

= $$64 + 216 = 280$$

Expression 1 :  5x - 1 < 3x + 2

=> $$5x - 3x$$ < $$2 + 1$$ => $$2x$$ < $$3$$

=> $$x$$ < $$\frac{3}{2}$$ --------------(i)

Expression 2 : 5x + 5 > 6 - 2x

=> $$5x + 2x$$ > $$6 - 5$$ => $$7x$$ > $$1$$

=> $$x$$ > $$\frac{1}{7}$$ ---------------(ii)

Combining above 2 inequalities, we get : $$\frac{1}{7}$$ < $$x$$ < $$\frac{3}{2}$$

Thus, the only integer value that $$x$$ can take = 1

Equation (i) : $$x - y = -6$$

Equation (ii) : $$x + y = 16$$

Adding above equations, we get : $$2x = -6 + 16 = 10$$

=> $$x = \frac{10}{2} = 5$$

Substituting value of x in equation (ii), => $$y = 16 - 5 = 11$$

$$\therefore$$ $$x^2 - y^2 = (5)^2 - (11)^2$$

= $$25 - 121 = -96$$

Expression : $$(4a^{2}+12ab+9b^{2}/(2a+3b)$$

= $$\frac{(2a)^2+(3b)^2+(2.2a.3b)}{(2a+3b)}$$

= $$\frac{(2a+3b)^2}{(2a+3b)}$$

= $$2a+3b$$

=> Ans - (B)

Given : $$(x+y)^{2}=xy+1$$

=> $$x^2+y^2+2xy=xy+1$$

=> $$x^2+y^2+xy=1$$ ------------(i)

Also, $$x^3 - y^3 = 1$$

= $$(x-y)(x^2+y^2+xy)=1$$

Substituting value from equation (i), we get :

=> $$(x-y)(1)=1$$

=> $$x-y=1$$

=> Ans - (A)

Expression : $$\frac{1+x}{1-x^4}\div\frac{x^2}{1+x^2}\times x(1-x)$$

= $$\frac{1+x}{(1-x^2)(1+x^2)}\times\frac{(1+x^2)}{x^2}\times x(1-x)$$

= $$\frac{1+x}{(1-x)(1+x)}\times\frac{1}{x^2}\times x(1-x)$$

= $$\frac{x}{x^2}=\frac{1}{x}$$

=> Ans - (A)

Let the three consecutive odd numbers be $$(x-2),(x),(x+2)$$

=> Product = $$(x-2)(x)(x+2)=1287$$

=> $$x(x^2-4)=11\times117$$

=> $$x=11$$ and $$x^2-4=117$$

$$\therefore$$ Largest of the three numbers = $$11+2=13$$

=> Ans - (C)

Given :  $$ab=6$$ -----------(i)

Also, $$a+b=5$$ -----------(ii)

Cubing both sides, we get :

=> $$(a+b)^3=(5)^3$$

=> $$a^3+b^3+3ab(a+b)=125$$

Substituting values from equation (i) and (ii)

=> $$a^3+b^3+3(6)(5)=125$$

=> $$a^3+b^3=125-90=35$$

=> Ans - (C)

Given : $$a=2$$ and $$b=-3$$

To find : $$27a^3 - 54a^2b + 36ab^2 - 8b^3$$

= $$(3a-2b)^3$$

= $$[3(2)-2(-3)]^3=(6+6)^3$$

=$$(12)^3=1728$$

=> Ans - (D)

Given : $$m+n=1$$ ------------(i)

Cubing both sides

=> $$(m+n)^3=(1)^3$$

=> $$m^3+n^3+3mn(m+n)=1$$

Using equation (i), we get :

=> $$m^3+n^3+3mn(1)=1$$

=> $$m^3 + n^3 + 3mn=1$$

=> Ans - (B)

Expression : $$( x - 5)^{2}$$ + $$(y - 2)^{2}$$ + $$(z - 9)^{2}$$ = 0

$$\because$$ If sum of three positive numbers is zero, then the numbers are equal to zero

=> $$(x-5)^2=0$$

=> $$(x-5)=0$$

=> $$x=5$$

Similarly, $$y=2$$ and $$z=9$$

To find : $$(x+y-z)$$

= $$5+2-9=-2$$

=> Ans - (C)

Given : $$x+\frac{1}{x}=6$$

Squaring both sides

= $$(x+\frac{1}{x})^2=(6)^2$$

= $$(x)^2+(\frac{1}{x})^2+(2.x.\frac{1}{x})=36$$

=> $$x^2+\frac{1}{x^2}=36-2=34$$

=> Ans - (C)

Solution 1:
As the answer is independent of variables and so we can assume values for x,y and z an solve
let x=1,y=-1,z=0 therefore x+y+z=1-1+0=0
$$\frac{(3y^2 + x^2 + z^2)}{(2y^2 - xz)}$$
=$$\frac{(3(-1)^2 + 1^2 + 0^2)}{(2(-1)^2 - 1*(0))}$$
=$$\frac{4}{2}$$
=2
Solution 2:$$\frac{(3y^2 + x^2 + z^2)}{(2y^2 - xz)}$$=k
$$(3y^2 + x^2 + z^2)$$=$$k(2y^2 - xz)$$
$$x^2 + z^2+kxz$$=$$2ky^2-3y^2$$
We know x+y+z=0
we can see that for k=2
we get $$(x+z)^{2}=y^{2}$$
x+z+y=0
Therefore value of k=2

$$x^3 + y^3 + z^3 -3xyz$$=$$(x + y + z )(x^{2}+y^{2}+z^{2}-xy-yz-zx)$$
$$x^3 + y^3 + z^3 -3xyz$$=$$(x + y + z )((x+y+z)^{2}-3(xy+yz+zx)$$
13-3(1)=(1)(1-3((xy+yz+zx)))
10=1-3(xy+yz+zx)
(xy+yz+zx)=-3

$$\left( \frac{1}{P^2} \right) + \left(\frac{1}{Q^2}\right)$$=$$(\frac{P^{2}+Q^{2}}{P^{2}Q^{2}})$$
=$$(\frac{(P+Q)^{2}-2PQ}{P^{2}Q^{2}})$$
$$P = 7 + 4\surd3$$
$$Q = 1/P$$
$$Q=7 - 4\surd3$$
P+Q=14
$$(P+Q)^{2}$$=196
PQ=1
$$(\frac{(P+Q)^{2}-2PQ}{P^{2}Q^{2}})$$=196-2
=194

Given x-4y=0
x=4y
x+2y=24
6y=24
y=4
x=16
$$\frac{(2x + 3y)}{(2x - 3y)}$$=$$\frac{(2*(16) + 3*(4))}{(2*(16) - 3*(4))}$$
=44/20
=11/5

$$(\frac{x}{a}) + (\frac{y}{b}) = 3$$
bx+ay=3ab
3bx+3ay=9ab
$$(\frac{x}{b}) - (\frac{y}{a}) = 9$$
ax-by=9ab
3bx+3ay=ax-by
3bx-ax=-by-3ay
x(3b-a)=y(-b-3a)
y/x =(a-3b)/(3a+b)
x/y=(3a+b)(a-3b)

As per the question,

$$x = a + \frac{1}{a}$$ and  $$y = a - \frac{1}{a}$$

Squaring both side,

$$x^2 = (a + \frac{1}{a})^2=a^2+(\dfrac{1}{a})^2+2$$

Similarly

$$y^2 = (a + \frac{1}{a})^2=a^2+(\dfrac{1}{a})^2-2$$

Now, $$\sqrt{x^4 + y^4 - 2x^2y^2}=\sqrt{(x^2-y^2)^2}$$---------(i)

Substituting the values in the equation (i)

$$\sqrt{x^4 + y^4 - 2x^2y^2}=\sqrt{(x^2-y^2)^2}=\sqrt{(a^2+(\dfrac{1}{a})^2+2-a^2-(\dfrac{1}{a})^2+2)^2}=4$$

Given that,

$$(8x^3 - 27y^3) \div (2x — 3y) = (Ax^2 + Bxy + Cy^2)$$

But we know that,

$$a^3-b^3=(a-b)(a^2+b^2+ab)$$

So,  $$(8x^3 - 27y^3) \div (2x — 3y)=\dfrac{(2x)^3-(3y)^3}{2x-3y}$$

$$\dfrac{(2x)^3-(3y)^3}{2x-3y}=\dfrac{(2x-3y)((2x)^2+(2y)^2+2x\times 3y}{2x-3y}=4x^2+9y^2+6xy$$

Now, $$4x^2+9y^2+6xy=Ax^2+Cy^2+Bxy$$

Now, comparing both side,

$$A=4, B=6$$ and $$C=9$$

Now, substituting the values in the equation,

$$(2A + B - C)=(2\times 4+6-9)=5$$

We know that, If $$ a^3 +b^3 + c^3 = 3abc$$ then, a + b+ c= 0

Therefore,

We will have, x - 7  + x - 8 + x+ 6 =0

therefore 3x = 9

and x= 3

Given,          $$\ \frac{\ x^3-y^3}{x^2+xy+y^2}=\ \frac{\ 5}{1}$$

$$\ \frac{\ \left(x-y\right)\left(x^2+xy+y^2\right)}{x^2+xy+y^2}=\ \frac{\ 5}{1}$$

$$\ \ x-y=\ \ 5$$ .................(1)

and                  $$\ \frac{\ x^2\ -\ y^2}{x-y}=\ \frac{\ 7}{1}$$

$$\ \frac{\ \left(x+y\right)\left(x-y\right)}{x-y}=\ \frac{\ 7}{1}$$

$$\ \ x+y=\ \ 7$$ .................(2)

Adding both the equations we get

2$$x$$ $$=$$ 12

$$x$$ $$=$$ 6

From equation (1)  $$x-y=5$$

$$6-y=5$$

$$=$$>               $$y=1$$

Therefore       $$2x:3y=2\times\ 6:3\times\ 1=12:3=4:1$$

Let  a -3 = x

a = x + 3

Therefore

a - $$\ \frac{\ 1}{a - 3}$$ = 5

x + 3 - $$\ \frac{\ 1} {x}$$ = 5

x - $$\ \frac{\ 1}{x}$$ = 2

$$\left(x-\ \frac{\ 1}{x}\right)^3\ =\ 2^3$$

$$x^3-\ \frac{\ 1}{x^3}-3.x.\frac{\ 1}{x}\left(x-\frac{\ 1}{x}\right)\ =\ 8$$

$$x^3-\frac{\ 1}{x^3}-3\left(2\right)\ =\ 8$$

$$x^3-\frac{\ 1}{x^3}\ =\ 14$$

Given,       $$a+\ \frac{\ 1}{b}=b+\ \frac{\ 1}{c}=c+\ \frac{\ 1}{a}$$

Take     $$a+\ \frac{\ 1}{b}=b+\ \frac{\ 1}{c}$$

$$a-b=\frac{\ 1}{c}-\ \frac{\ 1}{b}$$

$$a-b=\ \ \frac{\ b-c}{bc}$$ .................(1)

Take      $$b+\frac{\ 1}{c}=c+\ \frac{\ 1}{a}$$

$$b-c=\ \frac{\ 1}{a}\ -\ \ \frac{\ 1}{c}$$

$$b-c=\ \ \frac{\ c-a}{ca}$$ ...................(2)

Take      $$c+\frac{\ 1}{a}=a+\ \frac{\ 1}{b}$$

$$c-a=\ \frac{\ 1}{b}\ -\ \ \frac{\ 1}{a}$$

$$c-a=\ \ \frac{\ a-b}{ab}$$ ....................(3)

Multiplying the three equations we get

$$\left(a-b\right)\left(b-c\right)\left(c-a\right)=\ \frac{\ b-c}{bc}\times\ \ \frac{\ c-a}{ca}\times\ \ \frac{\ a-b}{ab}$$

$$=$$>       bc. ca. ab $$=$$ 1

$$=$$>        $$a^2b^2c^2=1$$

$$a^2+b^2+c^2=2\left(a-b-c\right)-3$$

$$a^2+b^2+c^2=2a-2b-2c-3$$

$$a^2+b^2+c^2-2a+2b+2c+3=0$$

$$a^2-2a+1+b^2+2b+1+c^2+2c+1=0$$

$$\left(a-1\right)^2+\left(b+1\right)^2+\left(c+1\right)^2=0$$

Sum of squares are zero so each term is zero

$$\left(a-1\right)^2=0$$,  $$\left(b+1\right)^2=0$$,  $$\left(c+1\right)^2=0$$

$$a-1=0$$,     $$b+1=0$$,    $$c+1=0$$

$$=$$>  a = 1, b = -1, c =-1

Therefore a-b+c = 1-(-1)-1= 1+1-1= 1

$$\ x^a.x^b.x^c=1$$

$$\ x^{a+b+c}=x^0$$

$$=$$> $$a+b+c=0$$

$$a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)$$

$$a^3+b^3+c^3-3abc=0$$

$$a^3+b^3+c^3=3abc$$

$$\left(a^2+ab+b^2\right)^2=16$$

$$a^4+a^2b^2+b^4+2.a^2.ab+2.ab.b^2+2.b^2.a^2=16$$

$$8+2ab\left(a^2+b^2+ab\right)=16$$

2ab(4) = 16-8

8ab = 8

ab = 1

Given  a = 25, b = 15, c = -10

$$\frac{a^{3}+b^{3}+c^{3}-3abc}{(a-b)^{2}+(b-c)^{2}+(c-a)^{2}}$$ = $$\frac{(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)}{2(a^{2}+b^{2}+c^{2}-ab-bc-ca)}$$

=  $$\frac{a+b+c}{2}$$

=  $$\frac{25+15-10}{2}$$

=  15

$$a^2+b^2+\ \frac{\ 1}{a^2}+\ \frac{\ 1}{b^2}=4$$

$$a^2+b^2+\ \frac{\ 1}{a^2}+\ \frac{\ 1}{b^2}-4=0$$

$$a^2-2+\frac{\ 1}{a^2}+b^2-2+\ \frac{\ 1}{b^2}=0$$

$$\left(a-\ \frac{\ 1}{a}\right)^2+\left(b-\ \frac{\ 1}{b}\right)^2=0$$

Sum of squares is zero so both the terms are zero

$$=$$>    $$\left(a-\ \frac{\ 1}{a}\right)^2=0$$,     $$\left(b-\ \frac{\ 1}{b}\right)^2=0$$

$$=$$>         $$a-\ \frac{\ 1}{a}=0$$,            $$b-\ \frac{\ 1}{b}=0$$

$$=$$>                  $$a=\frac{\ 1}{a}$$,                     $$b=\frac{\ 1}{b}$$

$$=$$>                 $$a^2=1$$,                     $$b^2=1$$

Therefore  $$a^2+b^2=1+1$$ = 2

Given $$x^3+3x^2+3x=7$$

Adding 1 to both sides

$$x^3+3x^2+3x+1=7+1$$

$$\left(x+1\right)^3=8$$

$$\left(x+1\right)^3=2^3$$

Therefore,   x+1 = 2

x = 1

$$x^2\ +\ y^2-2x\ +\ 6y+10=0$$

$$x^2\ -2x+\ y^2\ +\ 6y+9+1=0$$

$$x^2\ -2x+1+\ y^2\ +\ 6y+9=0$$

$$\left(x-1\right)^2+\ \left(y+3\right)^2=0$$

Sum of two squares is zero hence both the squares should be zero

Therefore, $$\left(x-1\right)^2=0$$ and $$\left(y+3\right)^2=0$$

x = 1 and  y = -3

$$=$$>     $$x^2+y^2=\left(1\right)^2+\left(-3\right)^2$$

$$=10$$

Expression : $$\frac{1}{8}\left\{\left(x + \frac{1}{y}\right)^2 - \left(x - \frac{1}{y}\right)^2\right\}$$

= $$\frac{1}{8}\left\{\left(x^2 + \frac{1}{y^2}+\frac{2x}{y}\right) - \left(x^2 + \frac{1}{y^2}-\frac{2x}{y}\right)\right\}$$

= $$\frac{1}{8}\times\frac{4x}{y}=\frac{x}{2y}$$

=> Ans - (A)

Given,  $$x + \frac{1}{x} = 8$$

$$=$$>  $$x^2+1=8x$$ ...............(1)

$$\therefore\ \frac{5x}{x^2+1-6x}=\frac{5x}{\left(x^2+1\right)-6x}=\frac{5x}{8x-6x}=\frac{5x}{2x}=2.5$$

Hence, the correct answer is Option B

Given,

$$x+y=4$$ and $$xy=2$$

$$y+z=5$$ and $$yz=3$$

$$z+x=6$$ and $$zx=4$$

$$x^3 + y^3 + z^3 — 3xy$$ = $$\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)$$

= $$\frac{2}{2}\left(x+y+z\right)\frac{2}{2}\left(x^2+y^2+z^2-xy-yz-zx\right)$$

= $$\frac{1}{2}\left(2x+2y+2z\right)\frac{1}{2}\left(2x^2+2y^2+2z^2-2xy-2yz-2zx\right)$$

= $$\frac{\left(x+y\right)+\left(y+z\right)+\left(z+x\right)}{2}.\frac{\left(x^2+y^2+2xy+y^2+z^2+2yz+z^2+x^2+2zx-4xy-4yz-4zx\right)}{2}$$

= $$\frac{\left(4\right)+\left(5\right)+\left(6\right)}{2}.\frac{\left(\left(x+y\right)^2+\left(y+z\right)^2+\left(z+x\right)^2-4\left(2\right)-4\left(3\right)-4\left(4\right)\right)}{2}$$

= $$\frac{15}{2}.\frac{\left(4^2+5^2+6^2-8-12-16\right)}{2}$$

= $$\frac{15}{2}.\frac{\left(16+25+36-36\right)}{2}$$

= $$\frac{15}{2}.\frac{41}{2}$$

= $$153.75$$

Hence, the correct answer is Option C

Given,  $$p+\left(\frac{1}{p}\right)=2$$

$$\Rightarrow$$  $$p^2+1=2p$$

$$\Rightarrow$$  $$p^2-2p+1=0$$

$$\Rightarrow$$  $$\left(p-1\right)^2=0$$

$$\Rightarrow$$  $$p-1=0$$

$$\Rightarrow$$  $$p=1$$

$$\therefore\ $$ $$p\times p\times p=1\times1\times1=1$$

Hence, the correct answer is Option C

Given,  $$x+\frac{4}{x}-4=0$$

$$\Rightarrow$$  $$x^2+4-4x=0$$

$$\Rightarrow$$  $$\left(x-2\right)^2=0$$

$$\Rightarrow$$  $$x-2=0$$

$$\Rightarrow$$  $$x=2$$

$$\therefore\ $$ $$x^2-4=2^2-4=4-4=0$$

Hence, the correct answer is Option A

Given, $$A=\frac{x-1}{x+1}$$

$$A-\frac{1}{A}$$ = $$\frac{x-1}{x+1}-\frac{x+1}{x-1}$$

$$=\frac{\left(x-1\right)^2-\left(x+1\right)^2}{x^2-1}$$

$$=\frac{x^2-2x+1-\left(x^2+2x+1\right)^{ }}{x^2-1}$$

$$=\frac{x^2-2x+1-x^2-2x-1}{x^2-1}$$

$$=\frac{-4x}{x^2-1}$$

Hence, the correct answer is Option D